Executive Summary
Making decisions about trade-offs that only have distant, future ramifications, and deal in abstract projections can be difficult for clients. Yet while we can always revisit decisions as time passes, the reality remains that in order to establish a plan in the first plan, we need to assess such uncertainties and make some initial decision. Would you rather have a plan that has a little risk of spending cuts and a high probability of excess wealth, or a plan with lots of risk of spending cuts that is less likely to leave over wealth you failed to use during your lifetime, none of which will be relevant for years to come? How do you weigh the risk of spending cuts against terminal wealth, or the volatility of a portfolio against the future impact it may have on spending?
Recent research suggests a new way to evaluate these problems, adopting utility functions that have been applied elsewhere in economics to the financial planning world, and opening up a new body of research in the process. While we may still have a ways to go before utility functions become commonplace in planning, this may be an early glimpse at the future of how we craft recommendations for clients... at least, if we can overcome some hefty hurdles, first.
The inspiration for today's blog post comes from two recent articles in the Journal of Financial Planning: "A Utility-Based Approach to Evaluating Investment Strategies" by Joseph Tomlinson, and "Spending Flexibility and Safe Withdrawal Rates" by Michael Finke, Wade Pfau, and Duncan Williams. Both articles evaluated how clients make trade-off decisions, such as the decision to allocate between stocks, bonds, and immediate annuities (Tomlinson) or to elect a higher safe withdrawal rate that also has an elevated risk of a future spending cut (Finke et. al.). What was unique about the articles was their effort to quantify these trade-offs, not with traditional metrics like final wealth or probabilities of success from which the client can choose, but with a utility function.
What Is A Utility Function?
What is a utility function? Think of it as a mathematical way to quantify how a person evaluates decisions and trade-offs, by assigning values to give weight to the possible outcomes. For example, imagine I'm trying to decide what to eat for dessert, and I can choose between scoops of ice cream, or chocolate chip cookies. I might declare that the amount of satisfaction or enjoyment I derive from a scoop of ice cream is 1.5 times that of eating a chocolate chip cookie. Accordingly, I assign a utility weight of "3" to a scoop of ice cream, and "2" to a chocolate chip cookie (noting that a 3:2 ratio of ice cream to cookies maintains my 1.5 satisfaction multiplier). Notably, the numbers here are abstract - it could be 3:2, or 1.5:1, or 75:50 - what's important is the relative weighting, which shows my preferences for ice cream versus cookies. What's significant is that once you know my ice cream/cookie utility function, you can easily determine how much ice cream I need to have to outweigh the value of 3 chocolate chip cookies (at least 2 scoops), or how many cookies it would take to dissuade me from 4 scoops of ice cream (at least 6 cookies!). What if I have 5 cookies? Better than 3 scoops of ice cream, but not as good as 4! In other words, you can mathematically optimize my decisions between any ice cream/cookie tradeoff once you know the utility function.
However, utility functions are not constrained to my dessert habits alone. They are also relevant in evaluating financial decisions. What's notable about our financial decisions, though, is that we don't treat them all the same; in dessert terms, the value of gaining or losing a chocolate chip cookie or a scoop of ice cream actually depends on how many cookies and ice cream scoops we already have. This was shown in the famous (and ultimately Nobel-prize-winning) "Prospect Theory" research of Kahneman and Tversky, which revealed that the utility function that we typically use to make decisions in the face of uncertainty has some unique features. An example from their research (from Wikipedia) is shown below.
Drawing A Utility Function
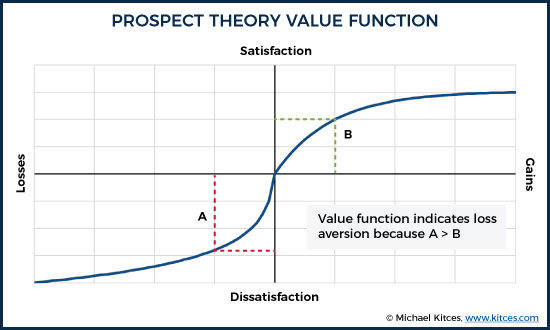What's so important about this utility function? First of all, the line flattens as you move to the right - more and more gains produce incrementally less positive personal value to us. This is the principle of diminishing marginal utility; if we have no wealth, going from $0 to $100,000 (a gain of $100,000) is a very big deal; going from $10 million to $10.1 million, not so much. Same wealth increase, different impact. And similar results apply regardless of whether we're talking about assets/wealth, or income levels.
Another important feature of this utility function is that the curve doesn't flatten quite so quickly on the losses side. In other words, even if our wealth or income keeps declining, it continues to have a negative impact on us, even when comparable gains in the opposite direction ceased to matter so much.
The third important feature of this utility function is that it drops more sharply just to the left of the center, than it rises to the right. This "kink" in the curve quantifies the reality that we experience more negative feelings about losses than we do positive feelings about comparable gains. For instance, the client who loses $100,000 feels more negative feelings than the client who gains a comparable $100,000.
Utility Functions In Practice
So why does all of this matter? Because we're not always very good at judging these trade-off preferences, especially far in advance. But if we know how to quantify them now with a utility function, it creates a unique opportunity for helping to craft recommendations, whether regarding asset allocation or retirement spending: we can mathematically optimize the "best" portfolio or retirement solution over the entire time horizon, giving proper weight not only to near term outcomes but to the consequences of future uncertain events as well. For instance, rather than just asking a client "would you like a 90% probability of success with a chance at $1.5 million remaining, or a 93% probability of success with a chance of only $1.2 million remaining" - which inherent asks a client to determine whether a 3% probability of failure is worth $300,000, even though our brains have no real tools to evaluate if that's a "good" trade-off - we can apply the utility function to help them quantify the decision more easily than having them do the abstract math in their head.
Accordingly, this is exactly what the Tomlinson article tries to do regarding the balance between stocks, bonds, and annuities, and what the Finke et. al. article does with respect to decisions about retirement spending and the risk of a spending decline. The outcome is a recommendation that won't necessarily be swayed by the inefficiencies and poor decision-making habits of our brains, but one that is mathematically optimized to be best given our preferences, as defined by a utility function.
The reality is that utility functions are not new to the analysis of economic and financial problems, but these research papers are some of the first instances that we have seen in trying to apply utility functions in the context of financial planning, and potentially represent a significant step forward in determining effective solutions for clients.
Caveats & Looking Forward
The caveat, though - and it's a HUGE one - is that in practice, it's very difficult to accurate define an individual's utility function, since by definition it is an abstract concept. Furthermore, it attempts to predict preferences in situations that the client may have never actually confronted. Can we know at what point do further income or wealth increases experience a significant decline in marginal utility, for a client who's never been wealthy enough to experience it in the first place? Is there a comparable diminishment for losses? Even if we're trying to generalize across all clients, what is the slope of the utility function, and how much convexity or concavity is there? Just how much more negativity does a loss generate than a comparable gain? After all, if you don't quantify the trade-offs correctly, you use the wrong utility function, which means are now optimizing the 'wrong' solution!
What this means is that in practice, utility functions at this point give us some new ways to think about problems, but probably shouldn't be relied upon too heavily. As Tomlinson points out, we lack formal survey research of individual preferences in retirement (not to mention pre-retirement consumption, income, and other aspects of the financial planning decision-making spectrum) to know how to precisely build the right utility function. It's also not clear just how much variability there is from one individual client to the next, and whether or how reliably a general utility function for 'most' people can apply to specific client circumstances. Nor are we anywhere close to having tools to try to identify a client's own individual and personal abstract utility function; as is, we still struggle in defining a client's basic risk tolerance, which itself is a form of utility measure (at least as it is applied to portfolio construction).
Nonetheless, what we're seeing here may easily be the front end of a new body of research, focused on trying to define the kinds of utility functions we use as human beings in making financial planning decisions, and then in turn re-evaluating the recommendations we provide as a profession and in specific client circumstances in light of those utility functions. Stay tuned for further developments.
So what do you think? Can you envision a world where we use utility functions to better quantify the difficult trade-offs that clients are often faced with? Could creating a client-specific utility function be part of the financial planning risk tolerance and data gathering process in the future? Do you find this kind of conceptual framework relevant when you consider how you work with clients?
