When Heuristics And Biases May Actually Improve Financial Decision-Making

In light of several decades of behavioral finance research, many people – perhaps particularly financial advisors – have been convinced that heuristics (i.e., a problem-solving approach using practical shortcuts that don’t necessarily consider all available information), and bias (i.e., a tendency toward some behavior or belief) are enemies of good decision-making. A ‘rational’ mind, we are led to believe, would eliminate all bias in order to make the best decisions possible. In fact, this messaging has been so popular among financial planning professionals, that many individuals now even market themselves as helping clients avoid biased decision-making. But do humans really make better decisions if they avoid heuristics and bias?

An interesting paper, Homo Heuristicus: Why Biased Minds Make Better Inferences, from Gerd Gigerenzer and Henry Brighton, argues that biases and heuristics have been overly demonized, and that biases and heuristics can actually often help us make better decisions than we would otherwise.

To be fair, it has always been acknowledged that there are costs associated with gathering information and engaging in the cognitive processes that are necessary for decision-making. And at some point, the marginal costs of acquiring and/or processing additional information that aids in our decision-making may not be worth the marginal benefits. From this perspective, heuristic shortcuts may prove useful when we are faced with insufficient resources or limited cognitive capacities, because even if we could get more information, the marginal benefit of that information wouldn’t make much of an impact anyway.

However, Gigerenzer and Brighton suggest that bias can actually improve decision-making beyond being a sort-of second-best approximation of more ‘optimal’ decision-making and that sometimes less truly is more. To support this idea, they use a different angle from the cost/benefit point of view: that the entire notion of an “accuracy-effort trade-off” is misguided, and that heuristics can help us achieve our goals, instead.

Heuristics In Human Behavior

If you have ever played baseball or softball (or have otherwise tried to catch a ball flying through the air), Gigerenzer and Brighton provide a good illustrative example of how heuristics can help us achieve our goals.

Imagine you are in the outfield and a ball is hit to you. How would you explain the process you would use to go about catching the ball?

If you are like most people, you probably don’t give much (conscious) thought to the process. You certainly don’t go through the process of conducting advanced calculations of a ball’s flight path, wind resistance, your body positioning, and the movements that will make your body intersect the ball’s flight path before it reaches the ground. Yet many of us can carry out the process as if we were making such calculations, and can actually catch the ball, even though we don’t really think about the process—we just intuitively do it.

Fortunately, researchers have developed some interesting ideas about how we actually carry out processes as ‘simple’ as catching a fly ball. For example, Gigerenzer and Brighton note that a key mental heuristic – the ‘gaze heuristic’ – actually helps to facilitate the catching process once a ball is high up in the air:

1. Fix your gaze on the ball;
2. Start running; and
3. Adjust your running speed so that the angle of your gaze remains constant.

If you have enough experience catching fly balls, you may be able to visualize catching one and realize that this is what you are in fact doing, even if you couldn’t previously articulate it. If we are successful in applying the gaze heuristic, we will end up getting our body to the right place needed to catch the ball while being able to ignore all of the variables we would need to use to calculate the trajectory of the ball.

Of course, this heuristic only applies to a ball that is already high-up in the air. Gigerenzer and Brighton suggest that we rely on a slightly different heuristic to position our bodies when a ball is still on an upward trajectory (“Fix your gaze on the ball, start running, and adjust your running speed so that the image of the ball rises at a constant rate”).

The key point, though, is that both of these heuristic techniques allow us to ignore all other factors, and that it’s not clear how (or if) performance would be improved even if we had the cognitive capabilities of carrying out the computations needed to calculate the trajectory of a ball in real-time. The gaze heuristic isn’t a problematic short-cut at all; in fact, it’s an incredibly helpful one that improves our ability to catch a fly ball.

Fitting vs. Predicting: Why Less Information Can Be More

To understand why less information can be more valuable when making decisions, it may be helpful to think about the difference between using statistical models to maximize fit, versus using them as predictive tools.

Gigerenzer and Brighton illustrate this distinction by using daily temperature data from London in the year 2000. Not surprisingly, there’s a U-shaped pattern in these weather data, with temperatures peaking in summer and reaching their lowest levels in winter. In Figure 3A below, from their paper, Gigerenzer and Brighton examine models fitting the weather data by graphing one line representing a 3^rd degree polynomial (dotted line in Figure 3A) and one representing a 12^th degree polynomial (solid line in Figure 3A). (For those who haven’t take a math class in a while, the more degrees there are in a polynomial, the more inflection points – or changes in the direction of the graph’s curvature – you can have when fitting a curved graph to the data.)

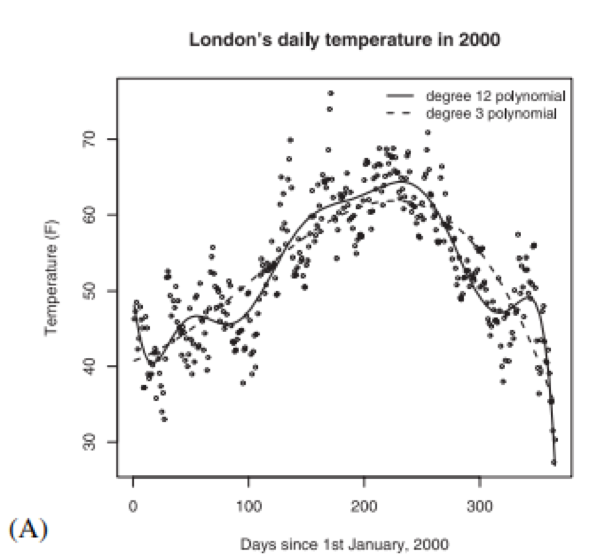
Fig. 3. Plot (A) shows London’s mean daily temperature in 2000, along with two polynomial models fitted with using the least squares method. The first is a degree-3 polynomial, and the second is a degree-12 polynomial.

Figure 3B shows that the 12^th degree polynomial fits the historical data better (i.e., in statistical terms, it has a higher R² value) than the 3^rd degree polynomial (compare the 3^rd and 12^th degree points on the solid line in Figure 3B). But even though it may seem as if the 12^th degree polynomial model (with its potential to have more curvature, and thus flexibility, in its shape) offers a ‘better’ method to analyze the data relative to the 3^rd degree polynomial model because of the better fit, it actually does worse at predicting future temperatures (compare the 3^rd and 12^th degree points on the dotted line in Figure 3B), because it ‘over-fits’ the data and we actually end up with a considerably more error-prone method than we would with the 3^rd degree polynomial!

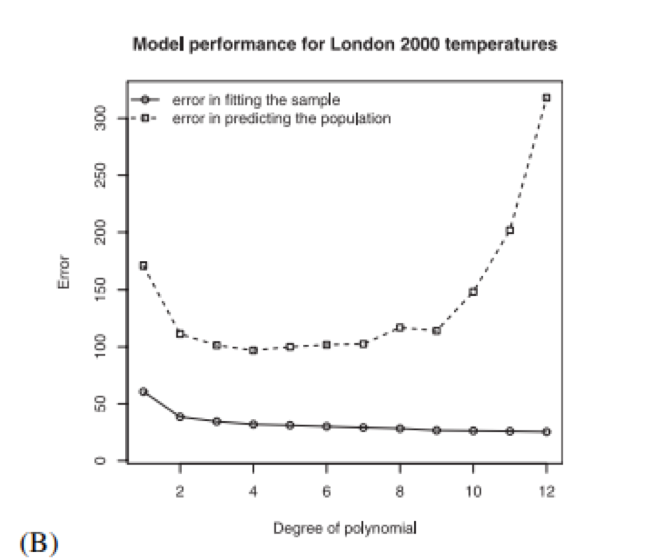
Fig. 3. Plot (B) shows the mean error in fitting samples of 30 observations and the mean prediction error of the same models, both as a function of degree of polynomial.

Interestingly, the 4^th degree polynomial actually performs the best as a predictor of temperature, as indicated by the dotted line in Figure 3B, which suggests a ‘sweet spot’ between models that are too simplistic and those that are too complex.

The key point, though, is simply to emphasize again that less can be more, and that even a detailed analysis of the existing data may not actually produce a better model than using a somewhat simpler heuristic. Because, as Gigerenzer and Brighton note, total error is comprised of ‘bias’ (i.e., systematic deviation in estimation due to the particular model we are using—in the case above, the polynomial chosen may be more or less biased in comparison to the true underlying weather pattern), ‘variance’ (i.e., how far data tend to spread out from their given average), and ‘noise’ (i.e., variability in the data that cannot be explained). With this in mind, calculating total error is done with the following formula:

Total error= (bias)² + variance + noise

Essentially, this formula suggests that bias is only one factor that contributes to total error. It’s too simplistic to say that bias is always good or always bad because the reality is that there is a trade-off due to error generated by bias and error generated by variance. Rather than avoid bias at all costs, we want to balance these factors that both contribute to total error.

To oversimplify the weather example, using a 1^st degree (i.e., a straight line) or 2^nd degree (one inflection point) polynomial to predict the weather will result in significant error due to bias, since temperatures don’t change on a straight line throughout the year (nor would they be expected to follow a pattern represented by a curve with only one inflection point, as in general there are at least two curves that shift weather direction, one in the fall and one in the spring). In other words, since these models fit very poorly to the historical data in the first place, the chances that they will reflect future temperatures with any accuracy is pretty low, and the bias resulting from selecting a 1^st or 2^nd degree polynomial model would hurt our ability to predict.

That being said, using a 12^th degree polynomial will – as we’ve already seen – overfit true underlying weather patterns, allowing the model to pick up significantly more error due to variance and noise, too. And these extraneous changes in the curvature of the predicted weather pattern won’t represent the true underlying weather pattern, explaining why using this higher-degree polynomial model to predict outcomes results in a much higher level of error.

Which brings us back to the key point that less (but not too little) really can be more.

Gigerenzer and Brighton cover other examples of when “less is more” in terms of prediction. For instance, to the authors’ own surprise at the time (they were still under the impression that while heuristics may be cost-efficient trade-offs, more data and processing would lead to better inferences), they (and others) used a “take-the-best” heuristic (a heuristic in which a single “most useful” factor is used to decide between options) and compared it to some of the best known predictive models, including tallying, multiple regression, and more advanced non-linear models, finding that when given tasks such as predicting which of two cities had the largest population, take-the-best outperformed or equaled all competitors. Furthermore, these findings were replicated across a varying set of contexts and datasets.

The ‘Ecological’ Rationality of Bias

While the use of bias may actually lead to better decision-making, it’s not always better than relying on more cognitively demanding approaches. And the degree to which bias can have a positive (or instead, a negative) impact will largely depend on one’s decision-making environment (e.g., the information, computational tools, and time available to make the decision). Simply put, whether a heuristic is ‘good’ or ‘bad’ will largely depend on the environment (or ecology) in which it is deployed.

There’s a lot of work to be done to improve our understanding of exactly which environments are best for using certain biases, but there is some evidence that people are good at ‘properly’ selecting biases that are ecologically rational given their circumstances (even though we can rarely articulate exactly what these are, or why we are doing what we are doing; see Gigerenzer and Brighton’s article for further examples and discussion). Evidence is also accumulating with respect to the use of biases and heuristics among other animals, pointing to some clear evolutionary implications regarding the development of biases, and continuing to suggest that evolutionary psychology may be more useful for understanding financial behavior than ‘behavioral finance’ in the long run.

For instance, Gigerenzer and Brighton give the example of male competition for mates among red deer stag as an example of the ways in which a progression of heuristics may be used in a manner that aligns with the availability of cues (i.e., information available) within one’s environment. As a stag is assessing whether to challenge a harem holder, the first cue available to determine which stag will be successful (i.e., is dominant) is often roaring, as this can be done by both stags from a considerable distance. If roaring doesn’t lead to either party backing down, the deer will move on to parallel walking in which the deer can size each other up. If that, again, doesn’t settle their dispute, only then will the deer engage in head-butting, which is the riskiest activity but also provides the clearest determination of which deer is physically dominant. Notably, in this case, the deer moved from low- to high-validity cues in trying to make their assessment – instead of just starting with the most ‘valid’ queue of fighting via head-butting to prove dominance – but this ‘inefficient’ approach to starting with less determinative (but also less risky) cues can ultimately promote the survival of each since there were multiple opportunities for either party to back down if the other was clearly dominant, and it was driven by environmental accessibility.

We can envision other examples where perhaps we have many cues and all are available at a rather low cost, but we aren’t quite sure how to weight the different cues in terms of validity. Consider, for instance, a consumer searching for a financial planner. There’s a fair amount of information about most financial planners easily accessible online (e.g., their education, experience, credentials, firm/employer, compensation model, background, etc.), however, some people may find it difficult to decide precisely how these various cues should be ordered (e.g., if one advisor is strong on experience and the other is strong on education, which is better?). Thus, instead of deciding based on one criteria, people may create binary categories of acceptable/unacceptable across a range of different cues, and then they’ll conduct their search until they identify an individual who meets two or more of their criteria (e.g., perhaps a CFP® with a clearly demonstrated niche of working with physicians).

Or perhaps some people do feel like they can weight different cues, and they decide to give a certain cue greater preference. For instance, it might be decided that education is twice as important as experience alone (or vice versa) and weighted accordingly. Or perhaps a good referral from a trusted colleague may trump all other cues and end an individual’s search process immediately.

While we still know very little about the cues individuals rely on when making decisions (particularly in highly specific contexts, such as working with a financial advisor), Gigerenzer and Brighton do provide a helpful table of well-studied heuristics, along with conditions under which a heuristic could be ecologically rational.

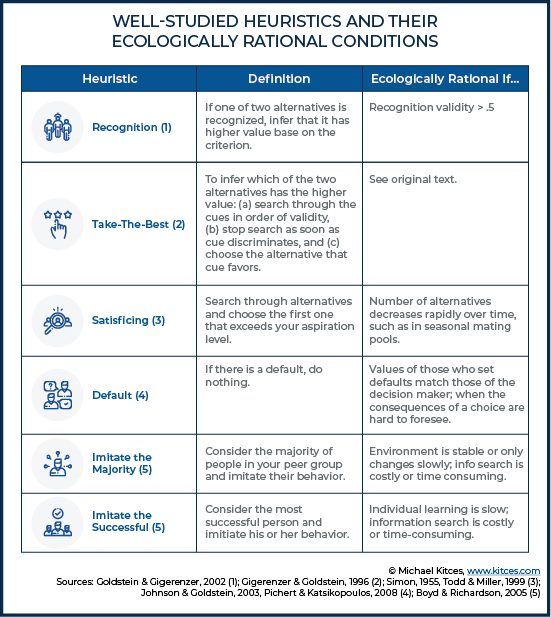
So, for instance, the “recognition heuristic” suggests that if you recognize one of two alternatives, the recognized alternative will be the better choice. And this heuristic may be “ecologically rational” (under the right circumstances) if the validity of the cue (i.e., the percentage of the time the cue provides the correct inference) is greater than 50%. The authors note that this particular heuristic has been applied effectively in predicting outcomes such as which individual will win a tennis match (and has performed equal or better compared to methods such as tennis rankings or expert seedings).

The Ecological Context For Financial Decision-Making

What may be most interesting to financial planners about Gigerenzer and Brighton’s work is the suggestion that heuristics outperform strategies that use more information and computation when (a) observations are sparse (i.e., we don’t have a large dataset of historical inputs/outputs to ‘train’ our model on), and (b) there is significant noise in observations (i.e., many of the data points that we do have don’t fit into any recognizable pattern). This is important because these are precisely the conditions under which humans make many financial decisions.

Many financial decisions we make have a significant impact on our financial well-being, but there aren’t often many data points available to help make that decision, and when there are, those data points often don’t have a recognizable pattern. Which means relying on heuristics may actually be very useful and appropriate!

Example 1: Ernie is 60 years old and wants to determine when he should retire. He envisions spending his retirement golfing together with a group of his best friends who share similar employment, spending, and other financial circumstances.

If it were possible for Ernie to retire hundreds of times, he might acquire enough observations to determine the best path based on the available data, and heuristics wouldn’t be necessary (giving way to more computationally demanding but available strategies). But absent that information, and given Ernie’s retirement aspiration, it can make more sense for him to use a heuristic method, such as “imitate the majority” (e.g., retiring at the same time most of your friends are retiring), and then to make any incremental adjustments along the way as necessary.

In Example 1, the “imitate the majority” heuristic may be a reasonable method for Ernie to employ, since he has a group of best friends with shared financial situations and retirement goals. But it’s important to note that the use of particular heuristics is highly dependent on situational context, and also prone to (potentially severe) error.

Example 2: Continuing the prior example, imagine that Ernie has an eclectic group of friends with different financial circumstances. Some were very successful entrepreneurs who retired very early in their 30’s, and some are still working part-time well into their 70’s. Nobody other than Ernie wants to play golf after they retire. In this case, the “imitate the majority” heuristic may be ill-advised, because there is no clear trend of the majority of Ernie’s friends. Instead, then, ‘imitate the successful’ may be a better heuristic for Ernie to rely on, by seeking out similar individuals who have successfully navigated the path he wishes to pursue, and then imitating their behavior instead.

In the context of having sparse information with no discernable pattern, it becomes less surprising that there are some strongly entrenched financial rules of thumb that many Americans rely on (e.g., save 10%) that are hard to argue against, provide at least a minimum level of prudence, and often really do get people more than close enough to their goals without doing a great deal of additional (time-demanding or costly) work.

Of course, many financial planners will run the numbers and conclude that our clients need to save more than 10%, but, excluding cases where people are getting a late start saving, this could actually be a case where experts are tending to overestimate how much is actually needed given that most financial planners (and the tools they use) do not account for how spending typically declines in retirement, and we also often fail to account for how more realistic earning patterns influence safe savings rates. In other words, it’s a scenario where the heuristic may actually be ample, while the calculational tools try too hard to fit the available data and add precision without necessarily increasing accuracy (akin to the weather model using a 12^th degree polynomial when the 4^th degree was not perfect but still best with the limited data available).

On the other hand, there are certain types of financial decisions involving robust data that we can be much more confident relying on. For example, decisions involving investment strategies, longevity assumptions, and other factors which provide a high number of observations (albeit perhaps with a high degree of noise, which may still be problematic, although there’s evidence that variability is declining in areas such as longevity), may be better suited for less heuristic-driven and more analytically-driven ‘optimal’ decision-making strategies.

---

Ultimately, the key point is that we shouldn’t treat bias and heuristics as something that should be avoided at all costs. We should think carefully about the environmental conditions in which bias and heuristics are deployed, and particularly pay attention to whether deploying additional cognitive resources will actually improve our ability to predict. If not—and particularly if additional cognitive resources actually reduces our ability to predict—then we should embrace the rationality of biases and heuristics.