Executive Summary
Since the turmoil of the financial crisis in 2008, financial planners have become increasingly obsessed about so-called "black swan" and "fat tail" events. As we witnessed one "impossibly rare" volatile day after another that fall, the fact that financial planning models its uncertainty using Monte Carlo analysis with normal distributions suddenly became not a virtue, but a liability. Yet for most clients, who don't invest with leverage, even a black swan event does not result in immediate destitution, but merely sets them on an unsustainable path that must be adjusted in the years that follow to prevent a subsequent depletion of assets. Which means in reality, it's not about more accurately modeling the probability of a black swan... it's about having a plan for dealing with it when the time comes.
The inspiration for today's blog post is some analysis of black swans that I have been working on as a part of my recent series on Monte Carlo analysis in the January and pending February issues of The Kitces Report. In exploring the increasingly common criticism of Monte Carlo analysis - that it is typically based on normal distributions that fail to accurately model black swan scenarios because the tails of the distribution are actually "fatter" and more leptokurtic than the normal distribution implies - I realized that in truth, we're spending far too much time worried about the wrong thing.
In the case of some engineering and physics problems (where the use of Monte Carlo was popularized early on), the results of Monte Carlo must be incredibly accurate up front because they will be used to determine the consequences of a nuclear reaction or the potential for a structural failure - which cannot be fixed after the fact. For example, an engineering scenario with a 98% probability of success and a 2% chance that a bridge could collapse would be deemed intolerable; the consequences are severe, and you can't adjust the strength of the bridge components once it's built. So the bridge is constructed to make the risk of failure as close to 0.00% as possible, and any exposure to black swans presents a real concern.
On the other hand, in the case of a financial planning scenario, a 98% probability of success actually just means a 2% likelihood that some change will have to occur to get the plan back on track before the end of the time horizon. The client is not bankrupt the day an "impossible" 10% market decline occurs; it's simply a financial loss that requires a future adjustment to the plan. In other words, 2% is not a measure of absolute failure; it's a measure of the probability of needing to make a future adjustment to get back on track. And the fact that the path can change along the way and that black swans are not automatically and instantaneously catastrophic means that we must view them differently.
Notably, in the case of many investment institutions, the problem is more serious, for one simple reason: leverage. In the case of a hedge fund or an investment bank, a precipitous short-term decline can be catastrophic. For instance, with 10:1 leverage, a 10% one-day "black swan" really can wipe out 100% of a fund's equity, leaving it worthless and leading any lenders to promptly call in their loans. The investment arrangement ends, permanently. In point of fact, this is exactly what happened to many hedge funds in 2008. But the difference is leverage; for a client, a 10% decline may literally be negligible to the long-term plan if the market recovers before the next withdrawal is due in a month or a year, while for a leveraged hedge fund, it means the fund is out of business at the end of the day, and next month or year will never come. Just ask Long-Term Capital Management (LTCM), who collapsed in 1998 when "black swan" events decimated its leveraged equity, even though the reality is that when the fund assets were ultimately wound up two years later, they had generally recovered their losses.
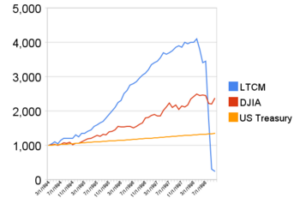For instance, the graphic to the right from Lowenstein's book "When Genius Failed: The Rise & Fall of Long-Term Capital Management" shows a comparison of 5 years invested in LTCM (with extensive leverage) vs "just" being fully invested in the Dow Jones Industrial Average. As the graphic clearly shows, when the "black swan event" finally did occur in mid 1998, it was genuinely catastrophic for LTCM, whose account balance essentially went to $0. The black swan event was unrecoverable. On the other hand, the decline for the unleveraged investor, as shown by the red line for the stock index, was little more than a tiny blip; at worst, the pullback meant cutting expenses modestly for a limited time, but it was not an immediate and total catastrophe by any stretch! The bottom line is that for an unleveraged investor, even a market black swan isn't that much of an immediate and permanent catastrophe, whether it's 1998 or 1987 or 2008.
Moreover, the reality is that because the risk of black swans is still rare - even though they are far more common than a normal distribution suggests - they still have a negligible impact on the plan up front. For instance, if the probability of success for a client's plan is 94%, but due to a more accurate analysis of potential black swan events "that proper takes into account fat tails and leptokurtic distributions" the client's probability of success is really only 92% (because an event that was supposed to be a once-in-a-billion-years event now has a 2% probability), the reality is that the client likely will not actually do anything different at that point! It's not a reason to make a dramatic change to spending or saving or to work another year. 92% is still awfully close to 94% (or 76% instead of 78%, or 86% instead of 84%, or any other 2% difference). In this scenario, "proper" accounting for black swans simply means a somewhat elevated likelihood (from 6% to 8%) that something will have to change down the road. In turn, this also means that getting the probability of success down to the last decimal point by using fancier, more robust distributions is somewhat unnecessary; knowing a client's probability of needing a plan adjustment is 8.1562% instead of 8% may be a more precise measurement, but it doesn't necessarily lead to a more accurate or materially different decision or actions.
In other words, with black swans in particular - given the fact that they are still rare - the real issue is ultimately not about the probability the client will have to make a change (which increases from impossible to "still pretty rare"), but about having a real plan in place for how the client's goals or actions will in fact be changed if the world begins to take the client down that improbable-but-concerning path (and doesn't recover in a timely manner). And of course, the reality is that such a plan for dealing with bad returns is equally relevant anytime the client's performance results lag too far behind - whether that's due to a black swan event, or a "white swan event" such as a mere decade of entirely probable below-average returns that gets the client dangerously far behind the original projection.
Your point is a good one, but I fear that there is a bit more to the story.
The key unknowns here are *how big* the “Black Swan” drawdowns will be, *how often* they should reasonably be anticipated, and thus the plausible margin of error of the Monte Carlo simulations. If, as in your example, the likelihood of error goes from 94% to 92%, the problem isn’t insurmountable. However, that presumed risk may well be much too low. The WSJ quotes Bill Bernstein in this regard as saying, “I take whatever probability of failure that comes out of your Monte Carlo simulation and add 20 percentage points.” Even if a 2% difference wouldn’t likely change my recommendation, a 20% difference is an entirely different magnitude of problem.
http://online.wsj.com/article/SB124121875397178921.html
Similarly, a 10% drawdown (the amount used in your example) can typically be accommodated in a reasonable retirement plan. But how about a 25% drop? 40%? More?
Bob,
I’ll be doing a follow-up blog to make this point further, but the reality is that we tend to grossly misjudge how frequent and severe these kinds of events really are. A 10-standard-deviation event like the daily market volatility in September/October of 2008 wasn’t even a 2-standard-deviation ANNUAL event.
That aside, I find the Bernstein quote to be beyond ludicrous. It doesn’t even make sense. What if my goal is to earn a 0% return and spend $10,000/year for 5 years from my mattress stuffed with $100,000. This goal will have a 99.99% chance of success, barring essentially hyperinflation. Would you arbitrarily add 20% to this probability “just ‘cuz”? It makes no sense.
That aside, a 25% drop is *NOT* a black swan. At all. It’s a completely normal market event. It’s not even a 2-standard-deviation event! In other words, 25% drops have NOTHING to do with black swans. They are ALREADY expected, with regularity, from a typical normal distribution! For that matter, even a 40% drop isn’t actually a black swan. In a world where equities have a standard deviation upwards of 20%, that’s barely a 2.5 standard deviation event. Which means you would absolutely expect it to happen a couple of times every decade. Which is exactly how often it has happened – once in the credit crisis of 1907, once in the Great Depression, and once in the credit crisis of 2008. Three times in a century, which is easily within the tolerance level predicted by a normal distribution alone.
The events you’re talking about are perfectly normal white swans. Not black ones.
Respectfully,
– Michael
Hi Michael —
I should have been more complete (always a pothole, especially within the context of a short reply).
As Taleb makes clear, we are far too eager to put the “Black Swan” label on all too common occurences. I agree on that point.
With respect to the Bernstein quote, I have no doubt that he was referring to typical portfolios and typical portfolio analytics (although I also suspect that your 99.99% success ratio estimate fails adequately to account for theft!). His point (and the WSJ’s) is that Monte Carlo simulations tend to underestimate large drawdown events, often by significant amounts. I see that as a major problem, especially on account of optimism bias and what Kahneman calls the “planning fallacy.” Moreover, as retirees age, their ability to “handle” these types of problems diminishes due to physical and mental health issues.
Since I all too infrequently see plans that can be expected readily to withstand large drawdowns during distribution (especially early on — whether “Black Swan” level or not), I would like to see much more effort spent trying to solve the “annuity puzzle” and less trying to figure out how we as advisors can somehow keep control of the money, despite clients’ general rejection of assured income options. But that’s just me….
With respect to your final series of questions, especially given the consequences of failure, I think we are seriously underestimating the potential for “Black Swan” and other large drawdown events in general or, perhaps more accurately, we are overstating our general ability to cope with such events.
Bob,
But this, combined with your prior comment, is part of my point here – things like 25% and even 40% drawdowns ARE part of the existing Monte Carlo framework!
The problem is that when we show the client has a 95% probability of success, that MEANS it’s at risk if a 1-in-20 event occurs, such as the kind of drawdowns you’re talking about, ARE in the analysis. Except we don’t typically create a plan of what to DO about that. We just acknowledge “yeah, 95% is pretty good” and move on, without any discussion of how we’ll handle the other 5% if it’s occurring. THAT is the point.
The kinds of bear markets discussed in the WSJ article ARE in Monte Carlo (at least when we model on an annual basis); but we do a terrible job of actually planning around and doing something WITH them. That’s the real issue.
Respectfully,
– Michael
I reckon there are approximately 5 kinds of black (or perhaps grey)swans. 1) precipitous market drops of anywhere from 20% – 50% (or more) that take anywhere from 1 – 3 years for the drawdown to be complete and another 1 – 3 years for there to be a complete or nearly complete recovery; 2) those that last longer (say from 5 – 10 years) and are accompanied by either a) inflation or b) deflation; and 3) those that last from 10 years to infinity (i.e. really is the end of the capitalist system) and are accompanied by either inflation or deflation and civil unrest.
It seems to me the preparation needed to deal with each of these is different.
Steve,
A 1-3 year drawdown of 20%-50% would not be a black swan. That’s well within a typical 1-3 standard deviation event that would be entirely probable from time to time under a normal distribution.
Depending on the parameters you put to it, #2 might be closer to a black swan. #3 – the end of capitalism – would certainly be a black swan event, but at that point I’m probably more concerned about my supply of food, water, and weapons, than my retirement plan. 🙂
Respectfully,
– Michael
Hi Michael —
“But this, combined with your prior comment, is part of my point here – things like 25% and even 40% drawdowns ARE part of the existing Monte Carlo framework!”
I agree with that point if it’s a good simulator – but many are not.
“The problem is that when we show the client has a 95% probability of success, that MEANS it’s at risk if a 1-in-20 event occurs, such as the kind of drawdowns you’re talking about, ARE in the analysis. Except we don’t typically create a plan of what to DO about that. We just acknowledge “yeah, 95% is pretty good” and move on, without any discussion of how we’ll handle the other 5% if it’s occurring. THAT is the point.”
And I agree with that one too. *My* (obviously inadequately made) point is not only that don’t we have discussions about and plans for those major drawdown events, but that when we do talk about and create such plans, they tend to be inadequate. Moreover, because of optimism bias and the planning fallacy, clients tend to hear “95% probability of success” as “you’ll be fine” (and assume that an x% “safe withdrawal rate” is really safe).
“The kinds of bear markets discussed in the WSJ article ARE in Monte Carlo (at least when we model on an annual basis)….”
Since there is no set Monte Carlo framework, that isn’t always so, unfortunately.
“…but we do a terrible job of actually planning around and doing something WITH them.”
I agree about the “terrible job” but add that even when we do create a plan to deal with large drawdown events, the plan is usually very poor.
Good points, Michael, as always. I view my role as financial coach to prepare my clients for these events mentally, emotionally and -as much as possible- financially.
At the end of the day, as one of my sisters says, “It’s just numbers on paper.” How we spend our days is how we spend our lives.
Black swans are by definition unexpected. Predicting the specifics of the next one is oxymoronic. The primary point is to expect something unexpected and therefor lowering your leverage etc.
Lee,
The point here is not predicting the specifics of the next black swan. In fact, the point is the opposite – your client should have a plan about how to respond to a dramatic market decline regardless, so that if/when a black swan ever occurs, you ALREADY know how to deal with it, regardless of the specifics of how it occurs. That’s the point of having a plan.
That aside, the overwhelming majority of clients whose plans fail are not due to black swans. They’re due to perfectly normal “white swans” like a merely below-average decade of returns. A true plan would/should capture those, too.
Respectfully,
– Michael
I have been using Riskalyze Pro to express the downside risk in client portfolios (for run of the mill corrections/crashes). My goal is to find each client’s pain number (a la kahneman) for planning and perspective purposes. The portfolio downside/upside range is used in all my client meetings (is an agenda item). Our job is to own the correct portfolio before the drops.
I have a different definition of a Black Swan event “an event that creates a swift 15%+ stock market drop – at a rate of over 50% annualized”