Why The Best P&C Insurance Deductible Is Driven By The Pseudo-Deductible Threshold For Filing A Claim

When Insurance Deductibles Are Exceeded: To Claim Or Not To Claim

When faced with a homeowners, renters, auto, or other property and casualty (P&C) loss, individuals can face a tough decision of whether to make a claim through their insurance, or simply absorb the cost themselves.

In the extremes, this decision is easy. When individuals face a loss smaller than their deductible (e.g., a minor scratch to a vehicle), there’s no reason to make a claim. We simply live with the loss, or absorb the entire cost to rectify the loss. Similarly, when a loss is very large relative to our deductible (e.g., a home destroyed by a fire), then we absolutely do make a claim – relying on our insurance to provide the financial security that it was intended for.

But things can get tricky for claims between these extremes – when claims are larger than one’s deductible, yet not large enough to be financially devastating.

If claims history did not influence the cost of insurance, we would simply make a claim for any loss above the insurance policy’s deductible. However, in the US, P&C insurance generally operates as a “bonus-malus” system, whereby insurance companies evaluate an insureds’ future risk profiles in part based on the tendency of policyholders to make claims (since experiencing losses and making claims is an imperfect yet reliable signal of experiencing future losses and/or claims). And, as a result, the potential impact of higher future premiums must be considered when evaluating whether to make a current claim.

Which means the decision of whether to claim or not to claim is not just a matter of whether the claim exceeds the deductible, but also whether the long-term benefit of forgoing a claim (and paying the cost out of pocket to avoid higher premiums) is more valuable than the long-term cost of making the claim (and paying higher premiums).

For instance, if an insured experiences damage to their vehicle which costs $1,100 to repair and they have a $1,000 deductible, then they likely will not file a claim, as the $100 benefit paid by the insurance company would likely not be large enough to offset the increased insurance premiums the individual is likely to face going forward for having made the claim. And, even in the event that an individual has “accident forgiveness” or similar protection built into their auto insurance policy, their “insurance credit score” (which includes claims history as well as some traditional credit factors) could be lowered, resulting in increased premiums of other P&C insurance, or a higher expense for acquiring other P&C insurance in the future.

This internal tension when deciding whether to claim or not to claim leads to what is known as a “pseudo-deductible” – referring to the true dollar amount of a loss one would need to experience before deciding to actually make a claim (above and beyond just the stated deductible itself).

How Pseudo-Deductibles Influence Our Behavior

The adoption of pseudo-deductibles is a largely under-investigated human behavior which is likely influenced by our attitudes, perceptions, and preferences toward risk. The concept was formally examined theoretically in a 1980 paper by Venezia and Levy, though the actual “pseudo-deductible” terminology comes from a 2006 Management Science article by Braun, Fader, Bradlow, and Kunreuther. In the latter study, the authors used homeowners insurance claims data from State Farm to provide empirical evidence supporting the idea that consumers engage in various claims behaviors which indicate the presence of a pseudo-deductible.

Unfortunately, the research since Braun et al.’s paper has been limited due to the fact that it is hard to measure claims that are never filed. However, a 2012 article by Dana Kerr was able to take advantage of a unique data set which specifically surveyed whether individuals had forgone making an auto insurance claim, as well as their motives for doing so (e.g., the amount was too small, didn’t want to raise their rates, etc.). Kerr’s analysis identified behavior consistent with consumer use of pseudo-deductibles in the auto insurance market, as a number of consumers reported not making insurance claims out of fear of increasing deductibles (or simply not being large enough claims to be worth the time and effort). In addition (and consistent with Braun et al.), Kerr found that both the size of a loss suffered and previous loss history were important factors in predicting whether a household would file a claim or not. Additionally, all else being equal, Kerr found that those who were younger and those who were female were more likely to be influenced by a pseudo-deductible.

Why Deductibles And Pseudo-Deductibles Are Distinct But Related

Despite the limited research on how pseudo-deductibles influence behavior, an intuitive notion of the concept has arguably been influencing consumer behavior for as long as P&C insurance has been around – albeit in a muddled and perhaps not fully sound manner.

For instance, insurance consumers may say to themselves, “I could take a $500 deductible, but I’m unlikely to make a claim less than $1,000, so I might as well take at least a $1,000 deductible. But, come to think about it, if I have a $1,000 deductible, I probably wouldn’t make a claim less than $2,500, so I might as well have at least a $2,500 deductible….” And so the process continues, until the consumer reaches a level at which they perceive themselves as likely to make a claim prior to reaching the next deductible threshold (and/or where they simply couldn’t afford to have a higher deductible), and set their deductible at this level.

In other words, not only does the pseudo-deductible phenomenon increase the threshold at which we will actually make a claim above the deductible, but it can lead to a circular process that causes us to increase the actual insurance deductible as well, which in turn drives the pseudo-deductible even higher, and so on… potentially further exposing a household to financial distress if there actually is a substantive claim (or at least forcing the household to carefully assess how high of a deductible, and pseudo-deductible, can truly be afforded).

Arguably, this logic is also embedded in the common advice to simply select as large of a deductible as one can afford. However, this can be misguided. It is much better to think about the deductible and pseudo-deductible as distinct yet related concepts, and it is not necessarily the case that one’s deductible should be as high as he or she can afford.

How Deductibles And Pseudo-Deductibles Are Distinct

The logic for separately analyzing a deductible and a pseudo-deductible is straightforward: The deductible and pseudo-deductible decisions result in separate financial consequences for insureds.

As a starting point, consider the decision of whether to adopt a higher or lower deductible. The choice between various deductibles can be thought of as a wager of sorts, in which the implied odds of experiencing a loss triggering a claim can be derived from the differences in premiums offered by an insurance company (at least so long as we assume, for the sake of simplicity, that the insurance is actuarially fair, and that claims behavior does not increase future premiums…more on relaxing this assumption later).

Consider the following example:

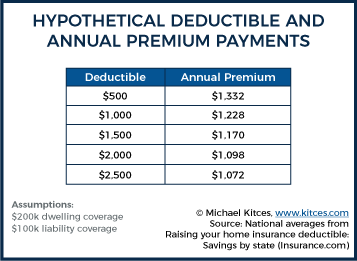
Example 1. Susan is shopping for homeowner’s insurance. Based on dwelling coverage of $200,000 and liability coverage of $100,000, Susan is quoted the following annual insurance premiums based on the deductible she is willing to adopt:

As you can see in the example above, Susan’s annual premium declines by $26 (from $1,098 to $1,072) if she increases her deductible from $2,000 to $2,500. For the sake of argument, assume Susan maintains a fairly modest amount of cash. Further, Susan is really averse to the idea of having her insurance rates increased, so she possesses a fairly firm pseudo-deductible of $2,500. In other words, no matter what her actual deductible, out of fear of increasing her premium, Susan simply will not file a claim for less than $2,500. Yet, at the same time, due to her cash limitations, Susan may need to file a claim for any losses higher than $2,500.

If Susan must choose from the options above, does this mean the $2,500 deductible is necessarily the best deal for Susan, since she’s willing to absorb losses as high as $2,500 anyway, yet cannot afford to absorb losses much higher?

Not necessarily. To understand why, it is helpful to first look at each decision she must make in isolation.

As noted earlier, when it comes to the deductible decision, Susan is effectively choosing between a set of implied wagers available to her, from which we can derive some implied probabilities of experiencing a loss. Again assuming that Susan is just contemplating either the $2,000 or $2,500 deductibles, Susan is facing two options with a premium differential of $26. Assuming real prices of all relevant goods and services remain constant, it would take 19.2 years ($500 / $26) without a loss in excess of her pseudo-deductible of $2,500 in order for Susan to come out ahead with the higher deductible, given the extra $500 she would have to pay out-of-pocket in the event that she did have a loss high enough to trigger her pseudo-deductible and an actual claim.

Or, to express this trade-off in terms of probability, the premiums offered imply that the probability of a loss exceeding Susan’s pseudo-deductible must be less than 5% ($26 / $500) in order for her to come out ahead with the higher deductible in the long run.

Notably, in isolation and assuming Susan had an excellent understanding of her risk profile (a questionable assumption), it would be this implied probability which actually drives the deductible decision. The outcome differential in the event of a pseudo-deductible triggering loss (-$500 under the scenario with the higher deductible) remains the same regardless of whether Susan has a $5,000 loss or a $300,000 loss. Similarly, the outcome differential in the event of not experiencing a pseudo-deductible triggering loss will always leave Susan $26 worse off in each year in which she adopts the higher deductible (premium of $1,098 versus $1,072).

Therefore, from a risk-neutral perspective and ignoring future premium increases due to claims behavior, the factor Susan should really focus on when deciding between these two options is whether she believes she is more or less likely to experience a pseudo-deductible triggering loss than the premiums quoted would imply. If she reasonably believes that a loss is more likely than the implied 5% odds, then she should take the lower deductible; if not, she should take the higher deductible.

Of course, assuming that an insurance company’s underwriters are good at their jobs, Susan is unlikely to know her own risk profile better than an insurance company. Which means, absent any fraud or solid basis for adverse selection on the part of a P&C insurance applicant (e.g., knowing about an additional risk or mitigating factor that was not disclosed to the insurance company), any belief that consumers have a better understanding of their loss profile is likely a misjudgment of risk due to some combination of having limited data, poor numeracy, or some behavioral bias. But this still doesn’t necessarily mean that Susan should ignore her lower deductible options and just go with the highest deductible option she can afford.

The Flawed Logic Of Conventional Wisdom To Take The Highest Deductible You Can Afford

Acknowledging the true factors driving the higher or lower deductible decision helps us see why the “take the highest deductible you can afford” approach is flawed.

First, just because one can afford a higher deductible doesn’t mean it provides the best trade-off given one’s risk preferences. Many wealthy investors can “afford” to be in 100% equities and would likely enhance intergenerational wealth through such an aggressive allocation, but that does not mean that 100% equities will provide the most value to them once accounting for all of the psychological costs and benefits of various strategies – including preferences to avoid both risk and uncertainty. Similarly, many ultra-wealthy investors could “afford” to replace their entire home if it burned down in a fire, but that does not mean skipping homeowner’s insurance and just retaining the risk will be their actual preference.

But suppose an individual is highly tolerant of risk and uncertainty. Does the highest deductible they can afford then become optimal?

Not necessarily. We cannot unequivocally say whether a $2,000 or $2,500 deductible is optimal for Susan. First and foremost, this is because we don’t what Susan’s risk preferences are (just because she can afford the $2,500 threshold doesn’t mean she’ll sleep well at night with it!), but we also cannot answer this question because there are reasons to believe either option could be suboptimal… because the optimal deductible isn’t only a trade-off unto itself, but something to consider relative to the pseudo-deductible as well.

On one hand, having a pseudo-deductible too close to one’s actual deductible can result in excessive claims behavior (as in the extreme, if the deductible and pseudo-deductible are the same, then the individual might file a “clearly” suboptimal $1 claim for being just over the threshold). On the other hand, it is necessarily true that the higher one’s pseudo-deductible, the lower their probability of experiencing a pseudo-deductible triggering loss (as the probability of experiencing a loss greater than $5,000 is necessarily less than the probability of experiencing a loss greater than $2,500). Of course, this is partially what makes a pseudo-deductible “work” in the first place (by avoiding excessive claims), yet it’s also possible to avoid too many claims, and end up underutilizing one’s insurance.

Of course, actuaries are not ignorant of this behavior (they understand it better than any of us). They price policies assuming that individuals understand these dynamics, and therefore behave accordingly. Which means, for Susan, the relevant reference point for determining the optimality of her pseudo-deductible is not simply the value of her pseudo-deductible relative to her deductible, but the value of her pseudo-deductible relative to the assumed pseudo-deductible actuarially priced into her premiums. Naturally, Susan cannot observe this amount assumed by her insurance company, but the reality is that if Susan’s pseudo-deductible is greater than the pseudo-deductible assumed by her insurance company, then the higher Susan’s pseudo-deductible (beyond that assumed by her insurance company), the more she is tilting the actuarial odds against herself.

In other words, à la Goldilocks, Susan is looking for a pseudo-deductible that is neither too high nor too low, but, instead, “just right”.

Which means, despite the fact that Susan may be willing to tolerate a loss up to $2,500, we can’t necessarily say whether Susan is better off with a $2,000 or $2,500 deductible given her pseudo-deductible of $2,500. In the former case, the gap between her deductible and pseudo-deductible may be too large, but, in the latter, it is almost certainly too small.

As a result, it is really the selection of one’s pseudo-deductible which must come first, because we must decide what we can actually tolerate and be financially capable of losing first.

Modeling An Ideal Pseudo-Deductible

While the deductible decision (in isolation, at least) can be reduced to a relatively simple wager, the reality is that choosing an ideal pseudo-deductible is actually far more complex. As Venezia and Levy noted, determining an optimal strategy for making claims decisions relies on a complex mathematical optimization method known as dynamic programming. The strategic process of balancing the costs of making a claim (higher future premiums) versus the benefits of making a claim (higher current compensation of losses) is far more difficult than just choosing between a menu of implied wagers (deductibles) based on one’s preferences for taking risk and avoiding losses.

Nonetheless, one way we can try and illustrate the real-world dynamics of selecting a pseudo-deductible is through Monte Carlo analysis. An inherent challenge of trying to model something like this is that, in the real world, consumers and insurance companies are always dealing with moving targets. As consumer behavior changes, so too does insurer behavior, and vice versa.

Nonetheless, we can still try our best based on some publicly available data. According to an InsuranceQuotes.com study from 2014, one particular factor which is relevant to premium increases due to claiming decisions is what type of claim an individual is making.

Average premium increases for a single claim ranged from a 14% increase due to liability claims due to bodily injury or property damage, to a low of 2% for weather-related claims. Intuitively, this makes sense, as, all else being equal, filing a liability claim is more likely to be indicative of some type of risky behavior or negligence than being struck by Mother Nature.

Combining the InsuranceQuotes.com premium increase data with data on the frequency and severity of homeowner insurance claims from an Insurance Information Institute report, we can arrive at the following parameters to use as a basis for a peril-specific Monte Carlo simulation.

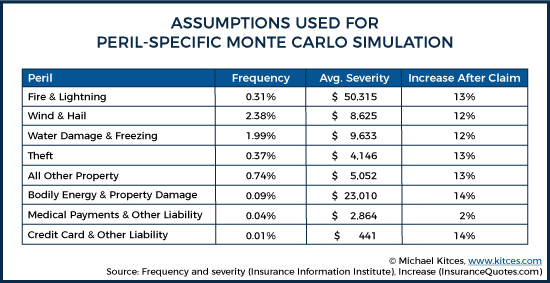
In this simulation, individuals were assumed to face perils consistent with the frequencies above over 60-year time horizons. Loss severities were assumed to be lognormally distributed according to the peril-specific means referenced. Additionally, premiums were increased as indicated for an individual with a claim in a respective category over 5-year rolling periods.

Consistent with real-world consumer dynamics, individuals in this simulation also faced premium increases when they had multiple claims in their recent past. While good summary data regarding how insurance companies penalize customers with multiple claims is harder to find, this simulation uses 5-year rolling history to determine penalties for those with multiple claims in recent history. If an individual had two claims in the past 5 years, they received an additional 25% increase in their premiums. For additional claims (up to a maximum of 5), a 50% increase was assessed for each successive claim.

(Notably, the frequencies used in this analysis assume only a 5.9% frequency of making any claim in a single year, resulting in roughly 1-in-5,000 odds of experiencing 3 losses in a 5-year period, roughly 1-in-80,000 odds of experience 4 losses, and roughly 1-in-1,360,000 odds of experiencing 5 losses in a 5-year period.)

Monte Carlo Simulation Results

As was mentioned above, we cannot unequivocally say whether Susan possessing a $2,500 deductible with $2,500 pseudo-deductible is better or worse than a $2,000 deductible with a $2,500 pseudo-deductible. This ultimately depends on how punitive insurers are within a malus-bonus system, as well as Susan’s risk preferences. However, we can begin to evaluate the financial considerations by simulating both scenarios in accordance with the assumptions discussed earlier.

Deductible/Pseudo-Deductible:

• $2,500 / $2,500
  • 60-Year Average Total Cost (Premiums + Losses) = $1,252
  • Standard Deviation of Total Costs = $103
• $2,000 / $2,500
  • 60-Year Average Total Cost (Premiums + Losses) = $1,255
  • Standard Deviation of Total Costs = $89

In terms of total cost, it appears that Susan would (on average, over 10,000 iterations) come out ahead with a higher deductible. Notably, however, this comes with considerably higher outcome volatility for Susan. As a P&C consumer, Susan does not get 10,000 60-year periods over which she can average her results – she only gets one!

We can visualize this variability in the histogram below.

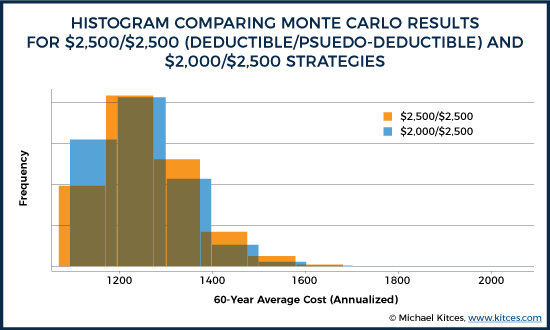
The orange bars ($2,500 / $2,500) exhibit both lower absolute values and a higher likelihood of experiencing more expensive sequences. We still can’t say whether one strategy is inherently better than the other (this depends on Susan’s risk preferences), but we can see that there are arguments for either strategy under consideration in this example.

Notably, however, this scenario did assume that Susan’s pseudo-deductible was fixed at $2,500 (i.e., her pseudo-deductible did not increase or decrease relative to her deductible). So what happens if we relax the assumption of a fixed pseudo-deductible and let Susan select among multiple pseudo-deductibles for a given deductible? How large should a pseudo-deductible ideally be?

A Monte Carlo simulation of 10,000 iterations at varying pseudo-deductibles reveals the following:

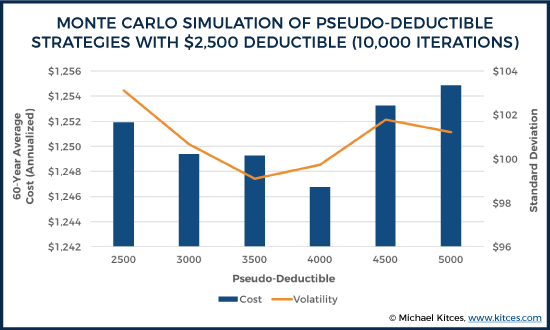
While there is undoubtedly a lot of noise here (even with 10,000 iterations losses are infrequent enough over 60-year time periods – about 3.5 per 60-year period – that the results don’t completely smooth out), we can see some general trends that conform with what we would anticipate: A u-shaped pattern through which both costs and volatility initially decline but then subsequently increase.

Based on the assumptions used in this analysis, it appears that an ideal pseudo-deductible (in terms of balancing both average long-term costs and volatility) with a $2,500 deductible may somewhere in the $3,500 - $4,000 range. Of course, there is noise in these results and the results are going to be highly sensitive to the specific assumptions made regarding future premium increases, but the results illustrate what we would expect conceptually (even if the question of precisely how much higher a pseudo-deductible should be in practice remains unanswered).

Additionally, we see a similar u-shaped pattern with a $2,000 deductible as well.

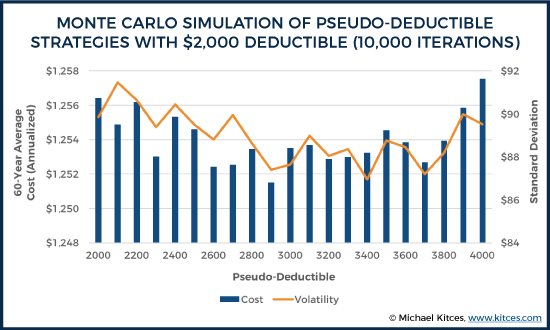
Notably, in the cases above, the results indicate an ideal pseudo-deductible may be somewhere around $900 above a $2,000 deductible. It’s important to not try and be overly precise here. Any particular point could still be considerably influenced by statistical noise, but it’s worth noting that the general relationships still apply. If a pseudo-deductible is too low or too high relative to a deductible, both average costs and volatility may increase. Notably, comparing the $2,500/$2,500 (deductible/pseudo-deductible) scenario against the $2,000 deductible scenarios with higher pseudo-deductibles, we find the following:

• $2,500 / $2,500
  • 60-Year Average Total Cost (Premiums + Losses) = $1,252
  • Standard Deviation of Total Costs = $103
• $2,000 / $2,900
  • 60-Year Average Total Cost (Premiums + Losses) = $1,252
  • Standard Deviation of Total Costs = $87

Which means Susan can attain the same average losses with a lower standard deviation by adopting a pseudo-deductible larger than her deductible.

Helping Clients Choose Pseudo-Deductibles

One relatively simple way that financial advisors can help clients navigate these decisions is to simply to help clients lay out the numbers and consider alternatives. In fact, a 2006 article by Eden and Sonsino in the Journal of Insurance Issues found that when individuals were given information about the probability of losses reoccurring, they made claims decisions which better aligned with more efficient claiming strategies. Specifically, when participants in an experimental study were given information about the likelihood of a hypothetical loss reoccurring, they increased their pseudo-deductibles (but not their deductibles!) to levels which more effectively balanced the long-term costs and benefits of filing a claim.

Therefore, one way financial advisors can help their clients adopt better pseudo-deductibles may simply be to help clients better understand the frequency and severity of claims they may face in the first place.

Of course, such claims are going to vary considerably from individual to individual, but simply helping clients move into a realm of more realistic base rates may be helpful. For instance, if clients think their odds of a $10,000 loss are 1 in 100 when in reality they are closer to 1 in 10 (using purely hypothetical numbers), then this should at least help move a client into a more realistic mindset for making risk management decisions.

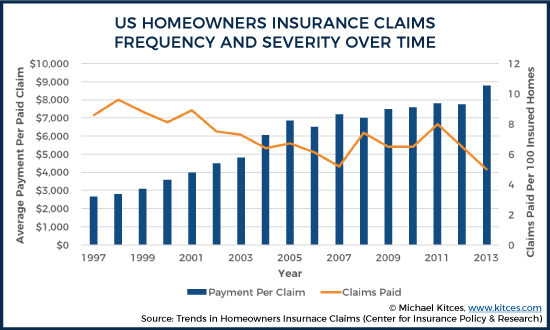
One potential source of such information is a 2014 report from the Center for Insurance Policy & Research on trends in homeowner’s insurance claims. According to this report, while the average number of claims per year per 100 insured homes fell from 1997 to 2013 (from 8.6 in 1997 to 5.0 in 2013), the average payment paid per claim during that period increased (from $2,676 in 1997 to $8,787 in 2013). Which means, on average, there was a 5% chance of a $8,787 claim among US homeowners based on the data analyzed (which implies a 5% chance of an even larger loss, since the $8,787 average claim is after also satisfying the deductible).

One challenge in conveying such information, however, is the fact that communicating probabilistic concepts can be difficult (particularly when advisors who commonly deal with such topics may unwittingly rely too much on jargon in trying to explain statistical topics to a client). Similar to how advisors should be careful when communicating the results of Monte Carlo analyses to clients, it is important that advisors communicate these ideas in a way that actually help a client make better financial decisions.

Additionally, there are some more general principles about selecting a pseudo-deductible which can also be noted. First, an optimal pseudo-deductible may not the be same at all stages in life. For instance, as an individual gets older (and therefore the number of remaining years of paying a higher premium are reduced), an optimal pseudo-deductible will likely decline. Second, deductibles and pseudo-deductibles should not necessarily remain constant. While risk preferences may be fairly stable over time (at least to some extent), one’s ability to withstand losses are not. Depending on how successful (or not) one is at building an emergency fund and adequately making progress towards one’s goals, one’s ability to withstand losses should change as well.

However, it is crucially important to help clients understand that one’s pseudo-deductible is an important starting point for selecting an ideal strategy. Choosing “the highest deductible an individual can afford” can be a costly strategy if this does not leave room for a higher pseudo-deductible that allows strategically avoiding some claims. Similarly, possessing an excessive aversion to using one’s insurance can result in negative financial outcomes as well. But both of these problems can be addressed when starting with a pseudo-deductible in mind.

Of course, identifying any precise threshold is impossible, as any solution at one point in time will be unstable due to future changes in consumer and insurer behavior. However, based on this analysis, a pseudo-deductible that is $500 to $1,500 above the deductible is a reasonable starting point for an ideal single-policy pseudo-deductible (or conversely, once a financially manageable pseudo-deductible is chosen, select an actual deductible that is $500 to $1,500 lower). Notably, one simplification of this analysis is that it looks at only homeowners insurance. However, in reality, claims in one P&C domain can influence premiums in other P&C domains. All else being equal, this would imply a higher pseudo-deductible than a single-policy analysis would indicate, but how much higher is ideal is a tough question to answer.

The key point, however, is simply to acknowledge that the determination of whether an individual should select a higher or lower deductible in P&C insurance is not as simple as taking the highest deductible that one can afford. While the optimization problem inherent to the pseudo-deductible decision is highly complex to ultimately solve, individuals should at least understand that the pseudo-deductible decision is generally optimized by first selecting a pseudo-deductible that is consistent with the individual’s tolerance and capacity for a potential claim, and then selecting a deductible that is lower than that threshold (to balance between the short-term benefits and the long-term costs of filing claims)!

So what do you think? Should the process of selecting a deductible start by selecting a pseudo-deductible instead? How do you help clients determine when they should make a P&C insurance claim? Please share your thoughts in the comments below!