Executive Summary
In the investment world, it’s common to discuss average rates of return, both in a backward-looking fashion (e.g., to report investment results), and in a more forward-looking manner (e.g., to project the average growth rate of investments for funding future goals in retirement planning software). However, the reality is that because returns are linked to each other – the return in one year increases or decreases the available wealth to compound in the subsequent year – it’s not sufficient to simply determine an “average” return by adding up all the historical returns and dividing by how many there are.
Instead of this traditional “arithmetic mean” approach to calculating an average, in the case of investment returns, the proper way to calculate average returns is with a geometric mean, that takes into account the compounding effects of a series of volatile returns over time. Which is important, because in practice the geometric average return is never as high as its arithmetic mean counterpart, due to the fact that volatility always produces some level of “volatility drag”, which can be estimated by subtracting ½ of the investment’s variance (standard deviation squared) from its arithmetic return.
Fortunately, the reality is that most investment returns, as commonly discussed by financial advisors, are already reported as geometric returns, typically stated as either a Compound Average Growth Rate (CAGR), an annualized return, or some similar label. Which means, intended or not, most financial advisors already project future wealth values in a retirement plan using the (proper) geometric return assumption.
However, the variance drain on a sequence of volatile returns still matters when financial advisors use Monte Carlo analysis, which by design actually projects sequences of random volatile returns (based on the probability that they will occur) to determine the outcome of particular retirement strategies. Because the fact that volatility drag is already part of a Monte Carlo analysis means that the return assumption plugged into a Monte Carlo projection should actually be the (higher) arithmetic return, and not the investment’s long-term compound average growth rate. Otherwise, the impact of volatility drag is effectively counted twice, which can understate long-term returns and overstate the actual risk of the prospective retirement plan!
The good news is that some Monte Carlo software tools, recognizing that most financial advisors report returns using the industry-standard geometric averages, already adjusts advisor-inputted return assumptions up to their arithmetic mean counterparts. However, not all Monte Carlo software automatically makes such adjustments. Of course, in many cases, financial advisors may wish to use lower return assumptions in today’s environment, given above-average market valuations and below-average yields. Nonetheless, advisors should be cognizant of whether they are unwittingly entering lower-than-intended return assumptions into their Monte Carlo retirement projections, compounding geometric returns in a manner that double-counts the impact of volatility drag!
Understanding Arithmetic Vs Geometric Return Averages
The most common version of an “average”, taught to children in their early school days, is known as the “arithmetic average” or “arithmetic mean” – where the arithmetic mean is calculated by (arithmetically) adding up all the individual items, and dividing by how many there are. Thus, for example, the average number of students in class is calculated by adding up all the students in all the classes and dividing by the number of classrooms, the average height of students in the class is calculated by adding up the heights of everyone in the class and dividing by the number of students, and the average score on the math test itself is calculated by adding up all the exam scores and dividing by the number of exam takers.
The arithmetic mean is effective in situations where each of the items being measured is independent of one another. The height of one student does not have any impact on the heights of the other students, and the exam score of one test taker doesn’t have any relationship to the others (assuming no cheating, of course!).
By contrast, in the world of investment returns, the results of one year are related to the results of the next, because both are being compounded on a dollar amount that grows in year 1 (by the returns of that year) before being reinvested (or continuing to be held for investment) in year 2. As a result, a simple arithmetic return fails to capture the compounding effects that occur from a sequence of investment returns.
Example 1. For the past 10 years from 2007 to 2016, the S&P 500 has had the following annual total returns: 5.49%, -37.00%, 26.46%, 15.06%, 2.11%, 16.00%, 32.39%, 13.69%, 1.38%, and 11.96%. The cumulative sum total of these returns is 87.54%, which would produce an average annual return of 8.75% over the 10 year time period. Which means a $10,000 investment would have grown to $23,144.74 over the 10 year time period.
Except it turns out that an actual $10,000 investment in the S&P 500 over this time period would have grown to only $19,568.08. Because the fact that the first year’s return was 5.49% meant by year 2, there wasn’t $10,000 invested to experience the -37% decline, there was $10,549. And by the third year, there wasn’t $10,000 (again) invested to experience the 26.46% recovery, as the portfolio would have been down to $6,645.87. And by the fourth year, the 15.06% return would have been experienced on only the $8,404.37 balance from the end of the prior year. And so forth.
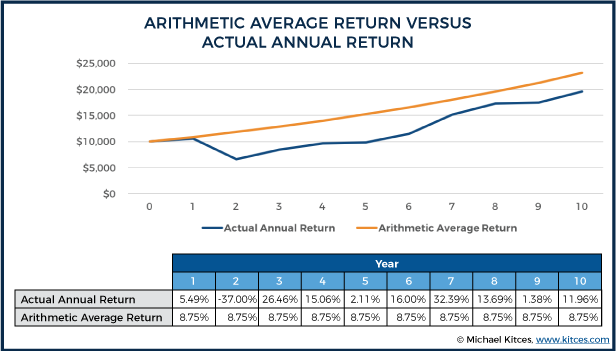
In other words, the fact that each year’s return carries over to impact the balance being invested into the subsequent year means it’s not enough to merely add up the returns of each year and divide by how many there are, to determine the average rate of growth the portfolio actually experienced. Instead, the actual average return is somewhat lower, to account for the fact that there were both higher and lower returns that compounded along the way. This is known as the geometric mean, or the geometric average return.
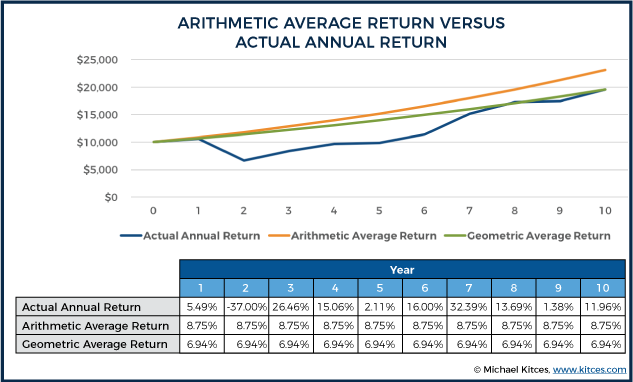
The geometric average represents the average annual growth rate that would have generated an equivalent amount of final wealth with a straight line series of returns, even though the returns didn’t actually occur in a straight line. Also known as the annualized return, or something the Compound Average Growth Rate (CAGR), the geometric average return may not match the actual return in any particular year, but by definition, it will compound into equivalent cumulative wealth at the end of the time period. In the earlier example, the geometric return or CAGR would have been 6.94%.
Volatility Drag: How Variance Drains Arithmetic Investment Returns
As shown in the example above, the geometric return was lower than the arithmetic average return, by about 1.81%, due to the fact that the compounded volatile returns with the early bear market never quite added up to what the straight line return would have been.
However, the reality is that this difference between arithmetic and geometric means isn’t unique to just this particular series of volatile returns with a bear market. In point of fact, any level of ongoing volatility will cause the geometric average to lag its arithmetic mean counterpart.
Example 2. Over the past 10 years (from 2007-2016), the annual returns of the Barclays Aggregate Bond index have been 6.97%, 5.24%, 5.93%, 6.54%, 7.84%, 4.21%, -2.02%, 5.97%, 0.55%, and 2.65%. Cumulatively, those returns add up to 43.88%, which would give the Barclays Aggregate Bond index an average annual return of 4.39%, and compound a $10,000 investment up to $15,364.05. However, in reality a $10,000 investment into this sequence of Barclays Aggregate Bond would have compounded to “just” $15,301.19, which is a geometric mean, or a compound average growth rate, of just 4.35% (not 4.39%).
Notably, in this example, the geometric average return was only very slightly lower than its arithmetic mean counterpart. Nonetheless, the fact remains that even with a less volatile sequence, that had only good compounding returns up front, the geometric mean was still lower.
The inevitable gap between the arithmetic mean and the geometric average return is often called “volatility drag”, because mathematically, the more volatile the returns are, the more of a gap there will be. Although the exact amount of volatility drag will vary by the exact sequence of returns and amplitude of the volatility, it can be approximated by subtracting ½ of the variance from the arithmetic mean (where Variance is the Standard Deviation squared, or conversely Standard Deviation is the square root of Variance).
Example 3. Continuing the prior examples, the standard deviation of the S&P 500 return series was 18.86%, which equates to a variance of 3.56%. On the other hand, the Barclays Aggregate Bond returns had a standard deviation of 3.12%, or a Variance of 0.10%. Accordingly, this implies that with an arithmetic average return of 8.75% on the S&P 500, the geometric return would be 8.75% - 3.56% / 2 = 6.97%, which is quite close to the actual geometric mean of 6.94%. Similarly, the Barclays Aggregate Bond had an arithmetic return of 4.39%, which would be reduced by 0.10% / 2 to an estimated geometric mean of 4.34%, which is very close to the actual geometric mean of 4.35%.
In practice, the estimation of the geometric mean from its arithmetic counterpart and the standard deviation (and variance) may not perfectly align, because a limited set of data points may not perfectly conform to the underlying normal distribution on which this formulaic assumption is based. Nonetheless, as shown in the examples above, it is typically very close – in this case, within 3 basis points for the geometric return of a 10-year series of stock returns, and within 1 basis point for the geometric average of the 10-year bond returns.
Retirement Projections And When To Use Arithmetic Vs Volatility-Drag-Adjusted Geometric Return Assumptions
While the impact of volatility on compounded arithmetic return is often called a “volatility drag” or a “variance drain” that reduces returns to arrive at a (lower) geometric average return, the reality is simply that the arithmetic mean is an inaccurate way to describe long-term compounded returns in the first place. Because it was never actually meant to describe the average of a series of interrelated “compounded” returns in the first place; it was/is intended to quantify the average of an independent series of data points.
Fortunately, in practice virtually all “returns” that are discussed in the context of investments are already based on the geometric mean. Whether it’s a Compound Annual Growth Rate (CAGR), or discussing the annualized returns. And both time-weighted and dollar-weighted returns are inherently measures of the compound rate of growth in a portfolio.
However, the fact that returns, as typically discussed, are based on geometric returns, means that financial advisors must still be cautious in how they translate rates of return into appropriate assumptions to use in forward-looking retirement projections.
Fortunately, when doing a traditional “straight-line” retirement projection, that estimates future wealth based on some average annual compound growth rate (and ongoing contributions or withdrawals), the geometric return is the appropriate return to use. As by definition, the geometric average return is the return that would produce the correct compounded dollars at the end of the time period.
However, when it comes to Monte Carlo assumptions, the proper return assumption is the arithmetic mean, not the geometric average return. The reason is that the whole point of Monte Carlo analysis is not just to estimate the straight line return to reach final wealth, but to actually project the results of a series of randomly drawn (and therefore volatile) returns based on the probability that they occur.
In other words, the gross (arithmetic) average returns that are plugged into a Monte Carlo analysis will automatically be reduced to the equivalent geometric returns in the process of projecting annual volatility. Which means if the geometric average return is the starting assumption, along with a standard deviation volatility assumption, and then a random series of Monte Carlo returns are drawn based on that underlying volatility, the end result will be retirement projections whose geometric returns are lower than intended.
Example 4. Jeremy is running a 30-year retirement projection for a 65-year-old client, where stocks are assumed to have an average annual growth rate of 10%, and bonds are assumed to grow at 5%, consistent with their long-term 90-year historical return levels. The standard deviations are assumed to be 17% and 5%, respectively. If these assumptions – of 10% returns and 17% standard deviation for stocks, and 5% returns and a 5% standard deviation for bonds – are plugged into the Monte Carlo analysis tools, the final geometric returns (due to volatility drag) will be approximately 8.56% for stocks and 4.75% for bonds (or slightly higher once a small positive impact for rebalancing is also included). Except, as just noted, the long-term geometric returns for stocks and bonds were supposed to be 10% and 5%, not 8.56% and 4.75%!
In order to achieve a Monte Carlo analysis where the final geometric return is consistent with the desired long-term averages, Jeremy should have gone back to the original data to calculate the (higher) arithmetic average on which the returns were based, or alternatively just increased the return assumptions by ½ of the variance to estimate the original arithmetic return. This would have produced an assumed (arithmetic) return of 11.45% for stocks, and 5.25% for bonds… such that, after including the impact of volatility drag, the final returns would have ended out at approximately 10% for stocks and 5% for bonds.
And notably, the cumulative impact of this difference is substantial. If the client had a 50/50 portfolio, the client’s long-term compounded returns would be only 6.65% (or slightly higher with a small potential rebalancing bonus), whereas they should have been 7.5%, which means the impact of volatility drag turns into a 0.85% reduction on actual long-term compounded returns.
In turn, this means that if Jeremy had planned to take a 5% initial withdrawal rate, a proper Monte Carlo analysis (based on historical arithmetic means) would have had an 87% probability of success (and the proper long-term compounded return), but one that used the geometric return upfront (as though it was an arithmetic mean, even when it isn’t!) would have only an 76% probability of success (with a long-term return substantially below what the geometric return was supposed to be)!
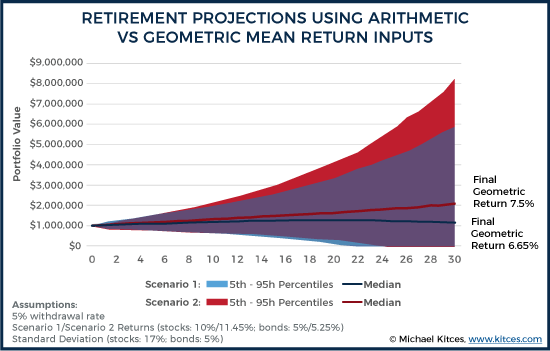
As the graphic above shows, when geometric returns are used as a Monte Carlo input, the final results produce lower returns than intended, resulting in a higher probability of failure, as the projection effectively double counts the impact of volatility drag. Because geometric returns already include volatility drag, and using geometric returns in a Monte Carlo projection just adds a second layer of volatility drag, when the software (re-)projects the future impact of volatility. By contrast, when arithmetic returns are used as the assumption up front, the final results are consistent with the geometric returns expected in the end anyway.
Of course, in today’s environment with high market valuations and low yields, many financial advisors may wish to use below-historical-average returns when projecting a retirement plan. Nonetheless, projecting reducing returns should be the result of an intentional desire to reduce returns, not a “lucky result” of mistakenly inputting geometric returns into a tool intended to calculate using arithmetic return assumptions.
On the other hand, the reality is that some Monte Carlo software tools already increased geometric returns to their arithmetic counterpart behind the scenes – using a version of the approximation noted above – recognizing that arithmetic returns are the proper assumptions, but that most financial advisors by default discuss and use geometric returns. Which means the software may actually be projecting correctly – having adjusted for the advisor’s default (geometric) return assumption. But at a minimum, it’s crucial to clarify, for any particular Monte Carlo retirement projection, what return assumptions are actually being used, and whether it is the (proper) arithmetic return being iterated on in the random Monte Carlo return draws.
The bottom line, though, is simply to recognize that there is an important difference between arithmetic and geometric return assumptions, both in the general case of describing and explaining returns (and the role of volatility drag), and especially given the unique effect that variance drain can have on Monte Carlo projections in particular… which makes it especially important to input the right version of a return assumption up front when projecting a retirement plan!
So what do you think? What are the return assumptions that you use in a retirement plan? Are they based on arithmetic or geometric average returns? Are you going to adjust your return assumptions going forward? Please share your thoughts in the comments below!
