Executive Summary
While no one likes to pay more in insurance premiums than they have to, an important fundamental principle of insurance is that in the end, there must be enough premiums (plus growth) to cover potential future claims (plus overhead and profits for the insurance company). Insurance coverage that is “too” cheap is actually risky, and coverage that is “expensive” is actually the most secure!
In fact, one of the most significant caveats to considering any form of insurance (or annuity) guarantee at all is if the insurance is not going to lose you money on average, it’s actually something to avoid. In other words, insurance guarantees should never be expected to make money on average for the policyowner, or the insurance company will lose money until it inevitably goes out of business and the guarantee will be gone anyway!
As a result, decisions to purchase insurance and/or seek out guarantees should always be viewed from the perspective of seeking to trade a small known loss to avoid a big unknown loss instead. The goal is not to finish with more money on average, but simply to shift the range of outcomes in a manner that increases the number of small losses and reduces the exposure to big ones that may be unrecoverable. So the next time you’re considering a type of insurance or annuity guarantee with a client, make sure you know why and how the coverage and guarantees are expected to lose money… and then decide if the trade-off is worthwhile anyway! And if you can't figure out how the guarantee will lose you money on average, it's a strong indicator that either you're missing a key detail and/or the guarantee is overpromising something it can't deliver, or the guarantee itself may be a mirage that the insurance company cannot possibly make good on in the end!
Fundamentals Of An Insurance Policy - Balancing The Premiums And Claims Equation
There are many types of insurance for an astonishing range of potential risks that can impact us, from the (financial) consequences of death to the danger of having a house burn down to the cost of a severe medical event. And while the potential consequences of such events could be quite financially damaging (or outright catastrophic) to any particular individual, the opportunity to pool together the risks of many people – knowing that some will experience the expensiveadverse event, but others will not – creates the possibility to turn a large unknown and potentially destructive risk into a more manageable known cost.
For instance, if there’s a 0.1% chance that a $300,000 house will burn down next year, then on average 1 out of every 1,000 people will have their house burn down – which means 999 people will be “fine” and the last one will face a catastrophe. To manage this risk, if each of the 1,000 people contributes $300 to a central pool of money (premiums), then collectively there will be $300,000 available to make whole the one person who has their house burn down (a $300,000 claim). Even if we don’t know exactly who is going to make the $300,000 claim (and which 999 will just be out their $300 bucks of premiums), as long as the payments in equal the anticipated payments out, we can collectively smooth out the risk for everyone, at a fairly 'modest' cost of $300 per person to insure against a $300,000 risk.
While this potential for risk pooling – where small premiums from a lot of people can provide for large payments to cover the risky events of a few, which in turn can be reliably predicted (on average) by relying on the law of large numbers – is the core principle of insurance protection, in the real world the implementation of insurance is slightly more complex. On the plus side, there is the reality that most risks play out over an extended period of time, which means that not every claim has to be paid directly and immediately with a dollar of premium collected, and instead some premiums can be invested for growth to cover future claims needs (and reduce the required current or future premium obligations). On the minus side, as the network of people and quantity of potential risks being insured grows, there is a need for some administrative overhead cost to manage the arrangement and the organization that implements it – an additional cost over and above just the payout of claims themselves. And in today’s modern world, where so many insurance companies are publicly traded companies owned by stockholders who expect the company to generate profits, the reality is that insurance companies need to ultimately need to have enough to cover claims (and overhead) that add up to at least a little less than they take in premiums (and generate in growth), so that there are so profits remaining. Which means the core identity formula for an insurance company is:
From the perspective of the person who buys the insurance coverage, this essentially means that their premiums (and the growth thereon) must collectively cover the claims that will be paid on the insurance, the overhead to run the insurance company, and the profits for the insurance company shareholders, as shown below.
The Savings Opportunity Of Self-Insuring
Understanding the equation of insurance from the perspective of the insured is important, because it also highlights the distinction between buying insurance and choosing to self-insure. When the “insurance company” part of insurance is eliminated, and the individual simply saves their own implied premiums (and grows them) to pay their own future “claims”, it removes the cost of the insurance company’s overhead, and the need for premiums to provide for the profits of the insurance company’s shareholders. Which means self-insurance can be simplified down to:
Since the premiums (and growth thereon) must only support the potential for future claims, but not the overhead of the insurance company and their desired profits, the formula above demonstrates why self-insurance is fundamentally a less expensive proposition than buying insurance, all else being equal. It saves the policyowner the cost of overhead and the “cost” of profits. (Michael’s Note: This also illustrates the relative appeal of mutual insurance companies, where the “profits” are redistributed back to the policyowners in the form of policy dividends that are a return of premiums, reflecting that the insurance can be cheaper in the long run when the policyowner is also the one entitled to the profits.)
Given the reality that purchasing insurance coverage should always require greater premiums than the “implied” premiums of simply self-insuring (where the insured simply sets aside money from personal assets to have that money, plus growth, cover the potential of the future “claim”), it’s generally best to avoid buying insurance coverage unless it’s genuinely necessary. Thus, why it’s typically beneficial to have larger deductibles if you can afford it (e.g., on homeowner’s or automobile insurance policies), implicitly self-insuring the “small” risks and just keeping insurance coverage for the “big” ones.
On the other hand, some potential losses are just so large that it’s not feasible to accumulate enough money to self-insure at all, which means buying insurance really does become the most effective route and skipping the coverage to self-insure is really just “gambling” that the risk won’t occur (because if it does, it would be a disaster). Choosing to purchase the coverage will be more expensive on average given that the risky event usually won’t happen (which means you’ll simply pay a premium and there’s no claim), and there’s a cost for overhead and the profits of the insurance company as well… but the trade-off may still be appealing, especially for claims that are potentially very large but with probabilities that are very small, which means the ramifications of being under-insured are severe (if the bad event occurs) but the actual cost of insurance can be rather modest. These scenarios explain why coverage like term life insurance for young people, or homeowner’s insurance, is so popular and effective.
Why Insurance Should Be A Losing Proposition
Insuring a risk is expected to be at least a little more expensive than self-insuring – both because of the implied cost of insurance company overhead and profits, and simply because with self-insuring there’s a possibility no “claim” (which you would pay from your own funds) will occur at all while buying coverage fixes the insured’s “share” of potential claims embedded in the premium itself. After all, when an insurance premium is paid, it implicitly covers both insurance overhead and profits, and a small slice of (likely someone else’s) future claims up front.
Nonetheless, the fact that the insurance policy puts you in a (slight) financially inferior position to self-insuring doesn’t mean it should be avoided. In fact, the only insurance coverage you should ever purchase is coverage that will lose you money on average!
The reason is that, as noted earlier, the essential equation for insurance must balance. Premiums and growth must equal the cost of claims plus overhead and the profits of the insurance company, because that’s all the money there is. In a situation where claims are expected to exceed the premiums and growth – in other words, the buyer of the insurance expects to make money on average by claiming on the insurance or guarantee – the equation can only balance in one way: given that overhead is generally fixed, the “profits” line item must go negative. In other words, the line can only balance if the insurance company has a sustained and ongoing financial loss and keeps bringing its own money to the table to cover those losses and make the sides balance!
Yet the problem with such a path in the long run is that if the insurance company is indefinitely incurring losses by paying out more than it receives in premiums (plus growth), eventually the insurance company is going to run out of money (reserves) to make the payments. The model is inherently unsustainable if outflows exceed income and there’s no way to replenish reserves. In other words, buying an insurance policy that is expected to come out ahead for the policyowner is the equivalent to buying an insurance policy from a company that is expected to go out of business. Which, of course, means that the financial outcome for the policy is not actually likely to be positive at all, and instead risks a total loss if the insurance company runs out of money before the risky event (and associated claim) actually occur!
Notably, the key point here is about averages, not individual claims. Clearly at least some individuals will receive more in claims than they contribute in premiums – with high-impact low-probability risk coverage like life or homeowner’s insurance, the claim if the event occurs could be many, many multiples of the premiums for that particular policyowner. Nonetheless, on average the (mathematical) expectation of anyone buying life or homeowner’s (or other) insurance is that they will receive back less than they pay in premiums (plus growth), either because they literally never have a claim or because (in the case of some types of coverage like automobile) there could be a small claim or few but still not enough to recover premiums (and associated growth). But again, there’s a key difference between potentially getting more in claims than were paid in premiums (because the risky event happens to you), and expecting on average to get more in claims than are being paid in premiums (plus growth); the former represents the essential principle of insurance, while the latter is an unsustainable path to bankruptcy (for the insurance company) and a potential total loss (for the policyowner).
Why It Can Make Sense To Buy Insurance Knowing It’s A Losing Proposition
While the key tenet of buying insurance is that it all should result in a financial loss on average (or else the insurance policy is unsustainable), that doesn’t make all insurance a losing proposition. Instead, it simply means that insurance should be targeted specifically for those situations where the risk would be so severe and catastrophic it’s either not feasible to have or save fast enough to self-insure it (e.g., the loss of earnings due to death or disability when you’re young), or it’s just too disruptive to other goals to self-insure it (e.g., a house that you ‘could’ afford to replace if it burned down, but it’s just far easier to manage a small premium than pay for a new house out of pocket if it really does burn down!). In other words, it makes sense to buy insurance where the premiums will result in a known small loss, if that small loss on average is still a better outcome than the possibility the big loss occurs instead. They’re both losses, but a small known can be far more manageable than a big (potentially catastrophic) unknown.
In essence, what this means is that buying insurance is not about improving your financial situation on average, but about narrowing the range of possible outcomes and eliminating the worst “tail” events. For instance, if the blue line in the chart below shows your potential wealth by just self-insuring, the red line shows how the results shift with insurance – where the outcomes are slightly worse in almost all situations, with a slightly lower probability of gains and a slightly larger likelihood of losses, but the small number of extreme events in the left (negative) tail are eliminated. This is the core trade-off of insurance: a slightly worse outcome on average, in exchange for the avoidance of a small number of really serious (albeit improbable) disasters that could happen.
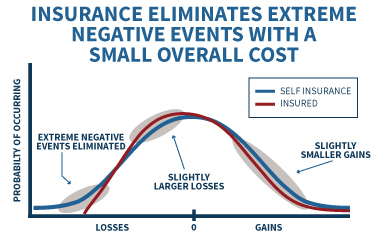
The key corollary to recognizing that it can make sense to buy insurance knowing it’s a losing proposition is that it’s equally important to avoid insurance that is expected to be a winning proposition (on average) – as again, by definition insurance companies that consistently pay out more than they take in will eventually end in ruin for those who get paid “last” and find out there’s no money left (precisely like a Ponzi scheme!). Guarantees that are cheap are actually risky, and guarantees that are expensive are actually the secure ones! If some form of insurance product, solution, or guarantee appears to improve your results across the board by giving generous benefits for a very modest cost, it really only means one of two things: 1) you’re missing a key cost, factor, or outcome, and it’s really not an improvement (or the guarantee is just overpromising something it can't deliver); or 2) the guarantee is accurate which means the product guarantee (or the entire insurance company) is doomed to failure in the long run and you could wind up with nothing!
Fortunately, the depth of insurance regulation means the scenario is far more likely to be #1 than #2 (insurance company defaults are blissfully rare in today’s environment). Nonetheless, the basic principle remains the same: be very, very wary of any insurance guarantee that implies you are expected to come out better most of the time, whether it’s a variable annuity with a guaranteed living benefit rider, generating “income” from equity-indexed universal life insurance, or a study that professes certain situations where long-term care insurance has a positive expected value for the buyer. Because in the end, either there are additional costly scenarios you’re missing that will make the outcome less favorable on average than you think and allow the insurance company to survive (for instance, sometimes what looks like insurance protecting against a loss is actually just a guarantee to return your own principal in the first place, while in other situations insurance companies hope you don’t realize what you’re giving up in foregone interest and opportunity costs), or the policy itself is at risk and can’t back the guarantees being provided (which certainly isn’t better!). Analyzing an insurance (or annuity) guarantee and believing it has a positive expected value on average generally means either you’re wrong, or you’ll lose (or both). That’s a time to run, not a time to sign on the dotted line!
In fact, ultimately the bottom line about insurance is simply this: if your insurance policy is expected to improve the outcome in all scenarios for a low cost and you can’t proactively identify how you’ll lose money (and the insurance company will make money) on average, you shouldn’t buy the insurance or annuity guarantee. If you can identify both what the “extreme” loss could be, and how much less you’ll finish with on average by buying insurance instead, and find that trade-off of the small known loss to be appealing enough to pay the implicit and explicit costs of insurance to avoid the big risky loss instead (because the low-probability big loss is so severe you must turn it into a smaller known loss instead), that is the proper time to buy the insurance guarantee... if it's still appealing at all!
